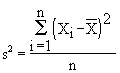 , sem agregação e
, sem agregação e 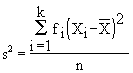 , com agregação.
, com agregação. Variância
Todas as medidas de dispersão anteriores são utilizadas ocasionalmente. Todavia, a medidas que abordaremos agora, são de longe as mais importantes, não só pelo seu maior uso, mas porque com o uso da média aritmética como medida de tendência central é natural as usarmos como medida de dispersão, e isto pode ser o motivo do seu amplo uso. Vimos que, para evitar o fato de que a soma dos desvios em relação à média é nula, definimos o desvio médio como a soma dos valores absolutos dos desvios. A dificuldade de se lidar, matematicamente, com valores absolutos fez a medida ser pouco usada no desenvolvimento da teoria estatística.
Outra forma de se evitar a soma nula é a elevação dos desvios ao quadrado. Como sabemos um número ao quadrado é sempre uma grandeza positiva, e os desvio negativos são transformados em positivos. A definição de variância como uma medida de dispersão segue esta linha de raciocínio e é calculada através da seguinte fórmula:
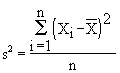 , sem agregação e
, sem agregação e 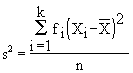 , com agregação.
, com agregação.
De muita utilidade no desenvolvimento dos estudos estatísticos, a variância tem uma desvantagem em termos de descrição dos dados, devido a falta de homogeneidade na unidade de medida utilizada quando comparada àquela da variável para a qual ela está sendo estimada; por exemplo, uma variável medida em reais, como é o caso de renda no nosso exemplo, terá variância medida em reais ao quadrado, o que é mesmo de difícil interpretação. A medida de dispersão discutida na próxima seção tenta resolver esta questão. Estimativas das variâncias das variáveis envolvidas são apresentadas a seguir:
Tabela 16 - Variância - Principais Variáveis
|
|
RENDA |
ANOSMORA |
ANOSANT |
EDUC |
SITUAÇÃO |
ESTILO |
|
Variância da amostra |
120983364,5 |
57,78019324 |
13,88792271 |
8,062318841 |
0,255072464 |
1,509661836 |