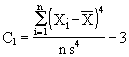
Medidas de Curtose
Algumas distribuições seriam bem caracterizadas, do ponto de vista da Estatística Descritiva, com as duas primeiras medidas apresentadas ( tendência central e dispersão). Vimos que as medidas de assimetria complementavam as informações verificando se os seus pesos eram distribuídos igualmente dos dois lados da média. Um medida menos usada, mas que completaria nossa discussão seria aquela chamada de curtose. Ela tenta medir o grau de achatamento das distribuições em relação á distribuição normal. A curtose de uma distribuição é dada pelas fórmulas:
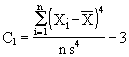
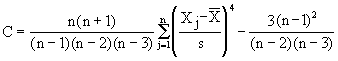

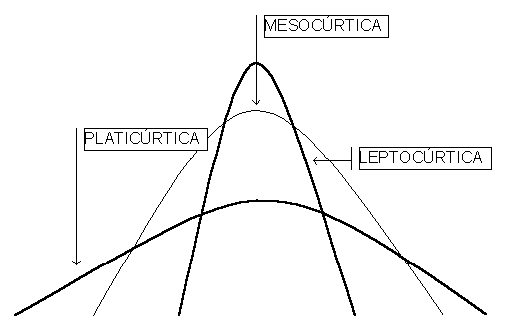
As duas primeiras dão medidas positivas ou negativas. Quando negativas é porque a distribuição é mais achatada do que a normal e são classificadas como platicúrticas. Quando as medidas são positivas ela são menos achatadas ou mais pontiagudas do que a normal, e são classificadas como leptocúrticas. As distribuições normais, ou próximas a ela, seriam classificadas como mesocúrticas e sua medida de curtose seria zero ou próximo de zero. No caso da terceira fórmula, a distribuição normal teria curtose igual a 3, as platicúrticas e leptocúrticas menor e maior do que 3, respectivamente. Fornecemos abaixo os valores de curtose para as variáveis do nosso exemplo e alguns gráficos que esclarecem o significado deste novo indicador para descrição das distribuições.
Tabela 20 - Medidas de Curtose - Principais Variáveis
|
|
RENDA |
ANOSMORA |
ANOSANT |
EDUC |
SITUAÇÃO |
ESTILO |
|
Curtose |
0,882207652 |
-0,734317413 |
5,337315305 |
0,214987514 |
-2,084554584 |
-1,453458302 |
De forma geral, quanto as medidas de curtose, as distribuições se classificam dentro dos padrões da seguinte Figura.
Figura 10 - CURTOSE