Medidas de Assimetria
Depois de analisarmos as distribuições através dos parâmetros que nos indicam sua tendência central e a dispersão das observações, podemos nos perguntar: Serão suficientes estas duas estatísticas para entendermos bem todos os aspectos de uma distribuição de freqüências? Vamos resumir o que as duas medidas anteriores nos proporciona em termo de informações, usando o nosso exemplo, mais especificamente sua variável renda. Obtivemos a informação de que a renda do bairro tem como média R$ 39827,39 , e que seu desvio padrão é de R$ 10999 . A mediana de R$ 36541,50 , nos diz que 50% dos imóveis tem rendas abaixo deste valor enquanto a outra metade as tem acima. Por que ela é menor do que a média? Além disso, verificamos que a moda é também menor que a média. Por que? Se elas fossem iguais, teríamos uma distribuição onde metade das observações estariam dividas abaixo e a outra metade acima deste valor, isto é dito pela mediana. Ao mesmo tempo, o peso das informações de altos valores seriam compensados pela aquelas de baixo valores no caso da média, pois ela está no centro da distribuição. Tudo isto nos leva a pensar em simetria, ou seja o que está abaixo da tendência central e o que está acima dela se comportam simetricamente. No entanto, suponha que, como é o caso da nossa variável renda, os grandes valores sejam maiores do aqueles pequenos; como a média, pelo que vimos antes, sofre a influência destes valores extremos, tende a ser maior do que a mediana. Quando isto ocorre, diz-se que a distribuição não é simétrica, ou que é assimétrica.
Isto pode ser visto a partir do histograma da variável Renda e aquele da variável Estilo (Figura 7 e Figura 8).
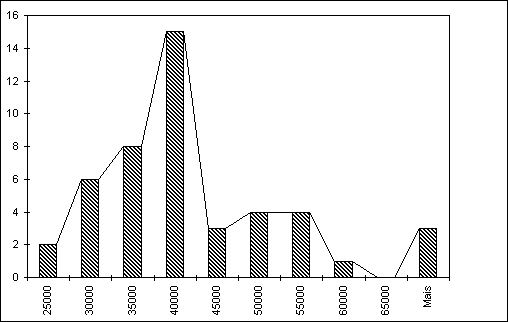
Figura 7 - Distribuição De Renda

Vemos que a primeira tem a cauda mais alongada para o lado dos maiores valores, e por isso se diz que a distribuição tem assimetria positiva, enquanto que a segunda tem uma cauda maior para a esquerda, e neste, caso se diz que a
Figura 8 - Distribuição De Estilos
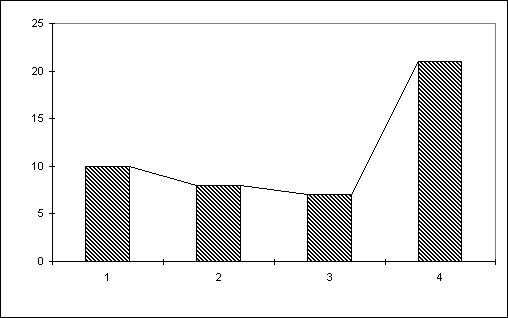
distribuição tem assimetria negativa. Estes valores podem ser verificadas na Tabela abaixo onde expomos medidas de simetria para as variáveis.
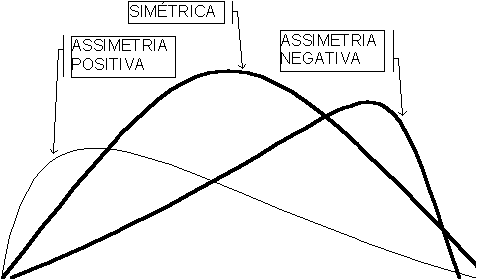
Então a noção de simetria é outro aspecto das distribuições que precisa ser levado em conta. De início verificamos que as distribuições podem variar de acordo com a "direção" da assimetria: quando a cauda maior da distribuição está à direita, dizemos que ela tem assimetria positiva; e quando ela está à esquerda, dizemos que ela possui assimetria negativa. No entanto, podemos ver que, mesmo que classifiquemos as distribuições com determinado tipo de assimetria, necessitamos de uma medida do seu grau, que pode variar mesmo tendo a mesma direção.
Apresentamos abaixo algumas das medidas mais comuns de assimetria que se propõem a fornecer tanto sua direção quanto o seu grau.
Aproveitando-se da observação de distribuições assimétricas os estatísticos propõem a seguinte medida para assimetria:
![]()
A segunda parte da equação, onde se usa a Mediana em vez da Moda, devido a maior facilidade de se estimar a primeira, é proveniente de uma relação empírica encontrada na maioria das distribuições moderadamente assimétricas. A medida mais utilizada e de maior precisão é dada por:
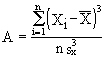
Quando só a mediana pode ser calculada ou se faz por ela a opção como medida de tendência central a seguinte medida é utilizada:
![]()
Na Tabela que se segue foram calculadas medidas de assimetria para as variáveis envolvidas com o nosso exemplo. Como podemos observar, os histogramas da variáveis Renda e Estilo, apresentados anteriormente geram coeficientes de assimetria positivo e negativo, respectivamente.
Tabela 19 - Medidas de Assimetria - Principais Variáveis
|
|
RENDA |
ANOSMORA |
ANOSANT |
EDUC |
SITUAÇÃO |
ESTILO |
|
Assimetria |
1,078566546 |
0,603112532 |
1,906152679 |
0,405944614 |
0,090000626 |
-0,448693302 |
Em geral, as distribuições são classificadas como tendo simetria positiva ou negativa, seguindo os padrões apresentados nas figuras abaixo.
Figura 9 - ASSIMETRIA