O Histograma
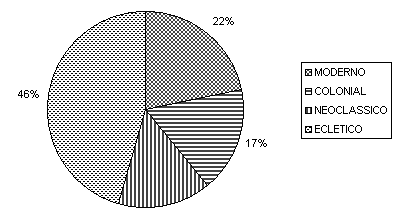
Outra forma, muito usada pelos estatísticos, de apresentação dos dados, é a forma gráfica. O tratamento gráfico, com o objetivo de clarificar o objeto de estudo, se desenvolve de várias maneiras. Há os gráficos puramente descritivos como a Figura 1, onde tentamos reproduzir a distribuição de freqüência do Estilo Arquitetônico no bairro, e há aqueles que, além de cumprirem este papel, também servem como instrumento analítico para estudos mais avançados sobre as variáveis. Um exemplo deste último tipo é o Histograma.
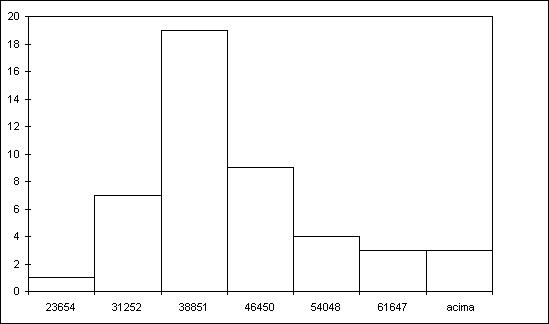
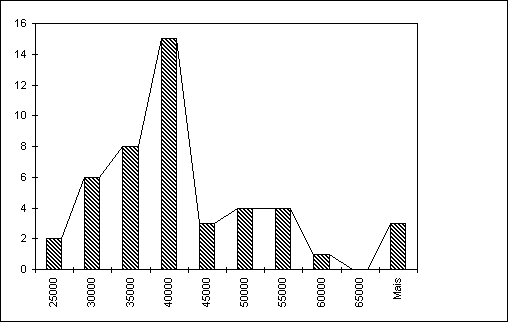
O histograma é um tipo de gráfico que tenta reproduzir uma distribuição de freqüência, tomando como base a idéia de incluir sob uma área especificada em eixos cartesianos o valor das freqüências observadas. Ele é um gráfico de barras como o reproduzido na Figura 2, para a variável Renda, cuja característica fundamental é que as áreas de cada barra são proporcionais à freqüência da classe representada por aquela barra. A Figura 2 se baseia na Tabela 9 onde se procurou um maior número de classes do que aquele representado na Tabela 4,
Figura 1- Distribuição do Estilo Arquitetônico.

para uma maior clareza do significado do Histograma. Atualmente esses gráficos são fornecidos pelos programas de computadores mas, para sua interpretação e uso analítico devemos esclarecer certos pontos básicos em sua elaboração.
|
Renda |
Freqüência |
|
23654 |
1 |
|
31252 |
7 |
|
38851 |
19 |
|
46450 |
9 |
|
54048 |
4 |
|
61647 |
3 |
|
acima |
3 |
Cada retângulo representando uma barra é formado por uma largura ou base (b) que é a parte que mede o valor da variável que está se tentando representar (eixo horizontal); uma altura (h) que representa as freqüências, ou o número de vezes que a variável toma valor naquele intervalo de classe, medida no eixo vertical. A área deste retângulo(A = b x h) deverá ser proporcional às freqüências de classe. Mantido isto, sempre pode-se escolher uma unidade para b de forma que h seja proporcional às freqüências ou mesmo iguais a elas, como apresentados na Figura 2. Feito isto podemos garantir que a soma das áreas de cada barra ou retângulo é igual a soma das freqüências.
Figura 2 - Histograma da Variável Renda.
Suponha então que tivéssemos um maior número de informações que nos permitisse diminuir os intervalos entre as classes e assim aumentando o seu número. É fácil imaginar que os retângulos ficariam muito mais estreitos e o seu número aumentaria muito como representado parcialmente na Figura 3. Se ligássemos os pontos médios do topo de cada retângulo por linhas retas teríamos os chamados polígonos de freqüência (Figura 4), o que nos leva a imaginar o caso no limite, onde teríamos larguras ou base tão pequenas que se confundiriam com os próprios pontos do eixo horizontal, o que nos levaria a um histograma ou polígono de freqüência representado por uma curva contínua para mostrar a distribuição, como exemplificado na Figura 5.
Figura 3 - Histograma da Variável Renda (> nš de classes).
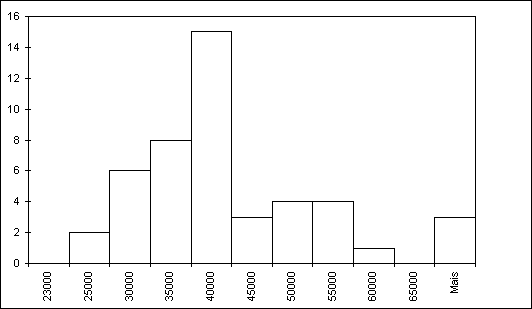
Figura 4- Histograma e Polígono de Freqüência.
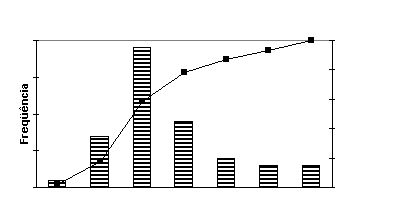
O importante a reter sobre este resultados é que podemos considerar a área embaixo desta curva, ou seja, entre a curva e o eixo horizontal como sendo igual á freqüência total ou número de observações. Além disto, e não menos importante, podemos fazer o mesmo raciocínio para a representação das freqüências relativas. Para elas podemos concluir também que a área abaixo da curva ou polígono de freqüência relativa é igual a soma destas freqüências, ou seja, igual a 1. Finalmente apresentamos (Figura 6), de uma forma diferente, o histograma para distribuição de rendas e um polígono de freqüências acumuladas, que é um outro conceito importante, e se aplica também às freqüências relativas; cada um dos seus pontos nos diz o número de observações "abaixo" daquele valor lido no eixo horizontal.
Figura 5- Histograma ou Polígono de Freqüência.
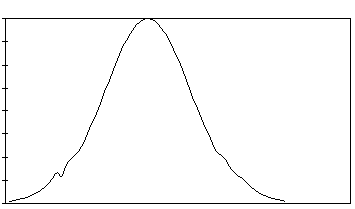
Figura 6- Histograma e Polígono de Freqüência Acumulada.