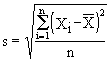 , sem agregação e
, sem agregação e 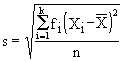 , com agregação.
, com agregação.Desvio Padrão
O desvio padrão surge como o caminho natural para resolver o problema de unidade de medida no caso da variância, e pode ser considerada a mais importante medida de dispersão, tanto pelo seu extenso uso quanto por algumas de suas propriedades, que comentaremos abaixo. O desvio padrão é definido como a raiz quadrada da variância e é estimado pela fórmula:
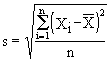 , sem agregação e
, sem agregação e 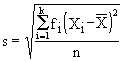 , com agregação.
, com agregação.
Pela coerência entre as unidades de medidas do desvio padrão e a variável analisada, essa medida funciona muitas vezes, como a própria unidade de medida. Por exemplo, pode-se demonstrar que o desvio padrão de uma variável y que seja definida como: y = aX + b é igual a |a|sx , onde sx é o desvio padrão de X; se definirmos a = 1/sx e b = -![]() /sx , então teremos a variável:
/sx , então teremos a variável: ![]() , que tem média igual a zero e desvio padrão igual a um. Essa última variável, que, como veremos, tem muitas aplicações, é chamada variável normalizada ou padronizada, ou mesmo "estandardizada" (do inglês standard). Outra importante propriedade do desvio padrão é aquela que nos diz que, se escolhermos qualquer número k, a probabilidade de
, que tem média igual a zero e desvio padrão igual a um. Essa última variável, que, como veremos, tem muitas aplicações, é chamada variável normalizada ou padronizada, ou mesmo "estandardizada" (do inglês standard). Outra importante propriedade do desvio padrão é aquela que nos diz que, se escolhermos qualquer número k, a probabilidade de ![]() é menor do que 1/k2. Isto gera algumas proposições muito comuns sobre o número de observações que caem longe da média aritmética em termos de desvio padrão. Por exemplo, para determinadas distribuições, pode-se garantir que 99% das observações estão no intervalo:
é menor do que 1/k2. Isto gera algumas proposições muito comuns sobre o número de observações que caem longe da média aritmética em termos de desvio padrão. Por exemplo, para determinadas distribuições, pode-se garantir que 99% das observações estão no intervalo: ![]() ou que 95% delas estão no intervalo:
ou que 95% delas estão no intervalo: ![]() . A Tabela seguinte nos dá os desvios padrões da amostra (ver nota 2), para as variáveis do nosso exemplo.
. A Tabela seguinte nos dá os desvios padrões da amostra (ver nota 2), para as variáveis do nosso exemplo.
Tabela 17 - Desvio Padrão - Principais Variáveis
|
|
RENDA |
ANOSMORA |
ANOSANT |
EDUC |
SITUAÇÃO |
ESTILO |
|
Desvio padrão |
10999,24382 |
7,601328386 |
3,726650333 |
2,839422272 |
0,505046992 |
1,228682968 |