![]()
![]()
...
![]()
![]()
![]()
![]()
...
![]()
![]()
![]()
![]()
![]()
...
![]()
![]()
...
...
...
...
...
...
![]()
![]()
![]()
...
![]()
![]()
![]()
![]()
...
![]()
![]()
CORRELAÇÃO E REGRESSÃO
Agora vamos imaginar uma tabela de distribuição conjunta de duas variáveis, X e Y, construída da seguinte forma:
Tabela 25 - Tabela de Correlação
|
|
|
... |
|
||
|
|
|
|
... |
|
|
|
|
|
|
... |
|
|
|
... |
... |
... |
... |
... |
... |
|
|
|
|
... |
|
|
|
|
|
... |
|
|
Nesta tabela os "f" indicam a freqüência absoluta, ou seja, o número de casos em que ocorrem simultaneamente os valores de X e Y. Essas variáveis são colocadas em ordem crescente de valores e podem representar intervalos de classe dos quais se toma o ponto médio. Mesmo intuitivamente pode se perceber que se os maiores valores de "f" estão em diagonal da direita para esquerda, isto indica que, em média, as variáveis devem crescer juntas, pois os maiores números de casos encontrados variam juntos, e no mesmo sentido das variáveis. Isto, em princípio, indicaria que elas estariam associadas positivamente, isto é, em média, variam juntas no mesmo sentido. Se, por outro lado, as maiores freqüências estão em diagonal da esquerda para direito, isto indicaria que quando uma variável cresce, em média, a outra decresceria; quando isto ocorre, dizemos que elas podem estar associadas negativamente. Pode ocorrer no entanto, que não haja nenhum dos padrões anteriores e as freqüências sejam espalhadas de uma forma mais ou menos errática pela tabela, isto indicaria uma não associação entre as variáveis; neste caso os estatísticos dizem que elas podem ser independentes.
Quando há um certo grau de dependência um dos objetivos da Estatística Descritiva é medir com que intensidade ele ocorre. Para fazer isto os estatísticos definem a seguinte medida expressa em diferentes formas:
![]()
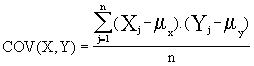
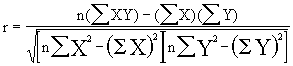
onde a primeira e terceira fórmula nos dão o coeficiente de correlação, e a segunda (que é usada em ambas, embora na segunda não explicitamente) define a covariância entre X e Y; os µ representam as médias aritmética das variáveis.
O Coeficiente de correlação varia entre -1 e +1. Se os dados estão associados, ou a partir de agora, correlacionadas positivamente ele será positivo e quanto maior for esta associação, maior será o seu valor que se aproximará de +1; quando ele é igual a +1, diz-se que a correlação é perfeita. O raciocínio oposto deve ser feito no caso de associações negativas. Quando ele é zero ou próximo de zero diz-se que as variáveis não estão correlacionadas ou são independentes.
Para verificar melhor o significado preciso do coeficiente de correlação, vamos voltar à tabela acima e usarmos o conceito de média aritmética visto anteriormente, calculando-o para cada linha ou coluna o seu valor. Como apresentamos a tabela, a variável X tem n valores e a variável Y tem m. Então, ao todo teremos n+m medias, n para Y e m para X. Por exemplo, para o valor de X igual a X1, teremos uma média para Y igual a ![]() ; da mesma forma, se tomarmos Y1, teremos a média dos X correspondentes:
; da mesma forma, se tomarmos Y1, teremos a média dos X correspondentes: ![]() . Chamemos estas médias de
. Chamemos estas médias de ![]() (j = 1, 2, ... n) e
(j = 1, 2, ... n) e ![]() (i = 1, 2, ... m), respectivamente. Podemos então, elaborarmos um gráfico onde, no eixo das abcissas colocamos os valores de X e nos das ordenadas os valores de Y. Nele poderemos marcar os pares ( Xj ,
(i = 1, 2, ... m), respectivamente. Podemos então, elaborarmos um gráfico onde, no eixo das abcissas colocamos os valores de X e nos das ordenadas os valores de Y. Nele poderemos marcar os pares ( Xj , ![]() ) e (
) e (![]() , Yi) resultantes do cálculo. Se os pontos relacionadas como os primeiros pares fossem representados por + e aqueles com o segundo por °
, o gráfico poderia ter os seguintes principais aspectos:
, Yi) resultantes do cálculo. Se os pontos relacionadas como os primeiros pares fossem representados por + e aqueles com o segundo por °
, o gráfico poderia ter os seguintes principais aspectos:
|
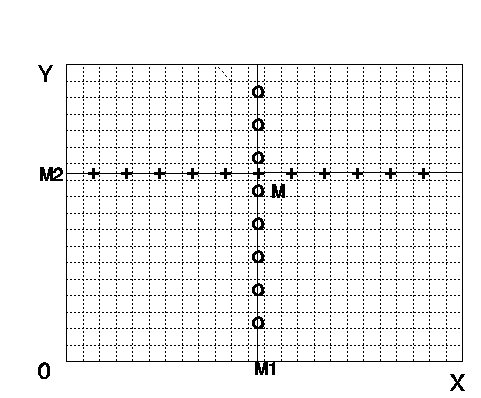
Figura 12- Independência |
Figura 13-Correlação Perfeita -Positiva |
|
Figura 14-Correlação Perfeita Negativa |
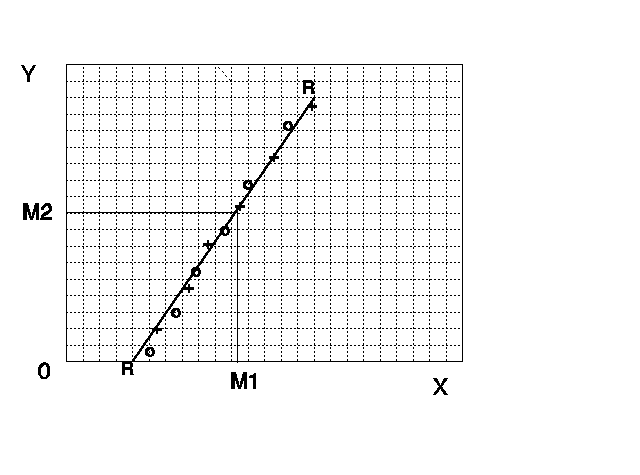
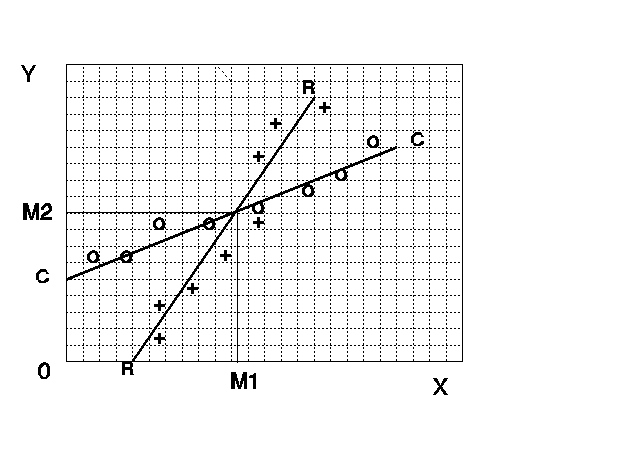
Figura 15 - Correlação |
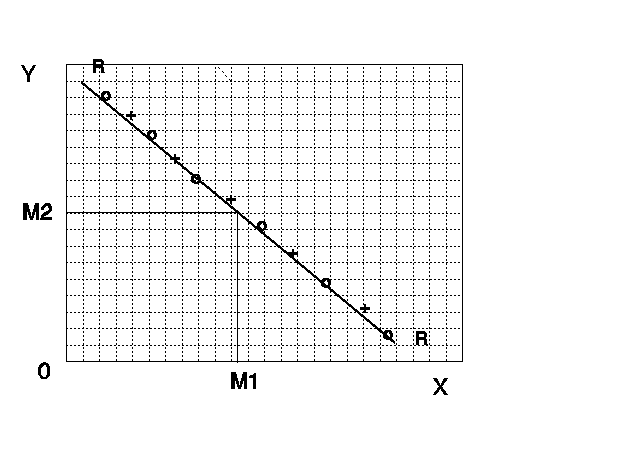
No primeiro caso teríamos todas as médias iguais para todos os valores tanto da variável X quanto da variável Y. Isto indica que os valores médios de uma variável não se modificam quando a outra varia. No linguajar estatístico dizemos que elas são independentes. No segundo caso vemos que quando X cresce de valor as médias dos Y também crescem, mesmo acontecendo com os valores de Y e as médias de X. Neste caso dizemos que há uma correlação alta e positiva entre as variáveis. No terceiro caso podemos ver um exemplo de correlação alta negativa.
Usualmente, o que acontece é um comportamento da forma representada no quarto gráfico no qual temos uma correlação positiva, mas não perfeita entre as variáveis. Nele podemos ainda observar que os pontos representando as médias podem seguir um padrão que nos proporcionaria uma possível previsão das médias de cada variável a partir das tendências nele observadas. Disto surgiu a idéia de unir esses pontos através de uma uma curva que melhor se adequasse aos padrões observados, como aquelas representadas por RR e CC no gráfico. Neste caso a tendência linear é marcante, mas nem sempre é assim; outra forma de curva pode ser mais adequada. A estas curvas chamamos de curvas de regressão e suas equações, quando referidas ao sistema de eixos, de equações de regressão.
Vamos supor, a partir deste ponto, que os dados se comportem de uma forma que a tendência linear seja a mais adequada e que estas curvas e equações tenham como padrões a linha reta. Neste caso podemos estudar melhor suas propriedades e melhor forma de estimá-las para quaisquer variáveis.
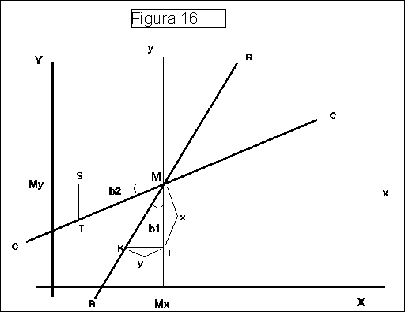
A Figura a seguir tenta esclarecer esta questão. As linhas RR e CC representariam o melhor ajuste linear ás relações entre as médias Y e X aos valores de X e Y, respectivamente. Por exemplo o ponto MY sobre a reta RR representa as coordenadas de um valor X (abcissa) e um valor médio dos valores de Y naquele ponto, que chamaremos ![]() . Para qualquer ponto X, teremos um valor correspondente sobre RR, que é a média dos valores de Y para aquele ponto. O mesmo raciocínio pode ser feito em relação à reta CC na qual as médias seriam representadas no eixo das abcissas. Pode-se demonstrar que MY e MX são iguais a
. Para qualquer ponto X, teremos um valor correspondente sobre RR, que é a média dos valores de Y para aquele ponto. O mesmo raciocínio pode ser feito em relação à reta CC na qual as médias seriam representadas no eixo das abcissas. Pode-se demonstrar que MY e MX são iguais a ![]() e
e ![]() , respectivamente. Além disso, se chamarmos de x = X -
, respectivamente. Além disso, se chamarmos de x = X - ![]() e de y = Y -
e de y = Y - ![]() , os desvio, em relação em média de X e Y, pode-se mostrar, com a ajuda do próprio gráfico, as seguintes relações:
, os desvio, em relação em média de X e Y, pode-se mostrar, com a ajuda do próprio gráfico, as seguintes relações:
|
(1) |
(1)’ |
|
(2) |
(2)’ |
|
(3) |
(3)’ |
|
(4) |
(4)’ |
|
(5) |
(5)’ |
As equações (1) e (1)’ são chamadas de equação de regressão de x sobre y e de equação de y sobre x, respectivamente. Elas também podem ser deduzidas a partir do métodos dos mínimos quadrados, que considera os erros de estimação como sendo aqueles provenientes da diferença entre uma linha reta do tipo: x=a1+b1y, na regressão de x sobre y ou, y=a2+b2y para o caso da regressão de y sobre x. Pode-se demonstrar que os valores de b1 e b2 encontrados anteriormente satisfazem a condição para que esta diferença seja mínima. Portanto pode-se interpretar as equações ou como sendo um forma de calcular um valor de x para um valor associado y (ou y em função de um associado x) de modo que a soma dos quadrados dos erros de estimação sejam mínimos, ou calcular a média dos x relacionada com um valor particular de y (ou a média dos y ligada a um valor particular de x) para que seja mínima a soma dos quadrados dos erros de estimação, contando cada média um número de vezes proporcional ao número de observações em que se baseia.
Usualmente os problemas de regressão são aqueles onde se considera distribuição de freqüência de uma variável quando outra é fixa em vários níveis. Isto é, para cada valor da variável x, observa-se a distribuição de freqüência de y, sendo a reta de regressão de y sobre x uma tentativa para ajustar melhor a média de y para cada valor de x. Por exemplo, suponhamos que quiséssemos saber como a educação do dono do imóvel influi na variável renda do nosso exemplo básico. Para isto, poderíamos escolher uma situação (fixar a variável x=EDUC) e verificarmos para ela quais os níveis de renda relacionados a esta situação. Fazendo isto para todos as situações poderíamos construir um diagrama de dispersão e fixarmos os pontos de média como visto anteriormente. Além disso, a partir dos valores encontrados pode-se estimar a equação de regressão pelas fórmulas acima, da regressão de y sobre x como Y=a2+b2X ou de x sobre y como X=a1+b1Y. Em todos os casos a variável que é fixada é aquela que é considerada independente, isto é, podemos fixá-la livremente no experimento ou na pesquisa e buscarmos a resposta da outra variável. Isto é colocado nas Figuras abaixo, e logo em seguida apresentamos as equações de regressão para as variáveis mencionadas.
Figura 17 - Dispersão e Reta de Regressão
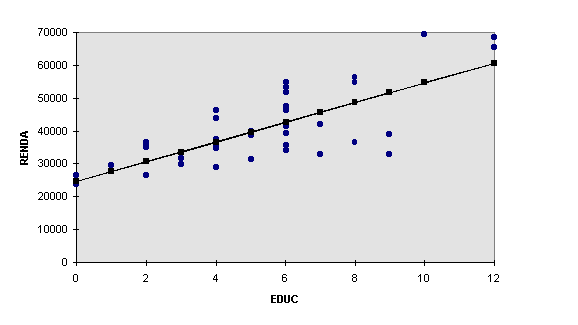
Figura 18 - Dispersão e Reta de Regressão
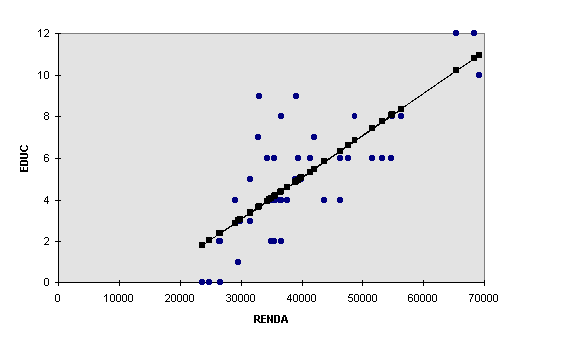
Equações de Regressão
EDUCAÇÃO = -2,92 + 0,0002*RENDA (X = a1 + b1Y)
RENDA = 24581,70 + 3009,87*EDUCAÇÃO (Y = a2 + b2X)
O coeficiente de correlação é usado para verificar o comportamento das duas variáveis sem que para nenhuma delas haja a hipótese de fixação pelo pesquisador. Portanto, podemos estimá-lo para qualquer situação envolvendo valores intervalares, enquanto as equações de regressão tem significado dependente dos aspectos teóricos envolvidos no campo onde elas estejam sendo aplicadas como veremos na parte referente a estimação de parâmetros. A seguir damos os valores do coeficiente de correlação e demais variáveis necessárias para os estudo da distribuição conjunta de algumas de nossas variáveis.
Tabela 26 - Valores Básicos de Regressão e Correlação
|
Média de Y(RENDA) |
39827,3913 |
|
Média de X(EDUCAÇÃO) |
5,065217391 |
|
Covariância |
23739,06144 |
|
Correlação |
0,776991108 |
|
Desvio Padrão Renda(Y) |
10879,02989 |
|
Desvio Padrão Educação(X) |
2,808389403 |
|
Variância de Y |
118353291,4 |
|
Variância de X |
7,88705104 |
|
Coeficiente de Regressão(b1) |
0,000200578 |
|
Coeficiente de Regressão(b2)) |
3009,878003 |
|
Constante (a1) |
-2,92327941 |
|
Constante (a2) |
24581,7049 |